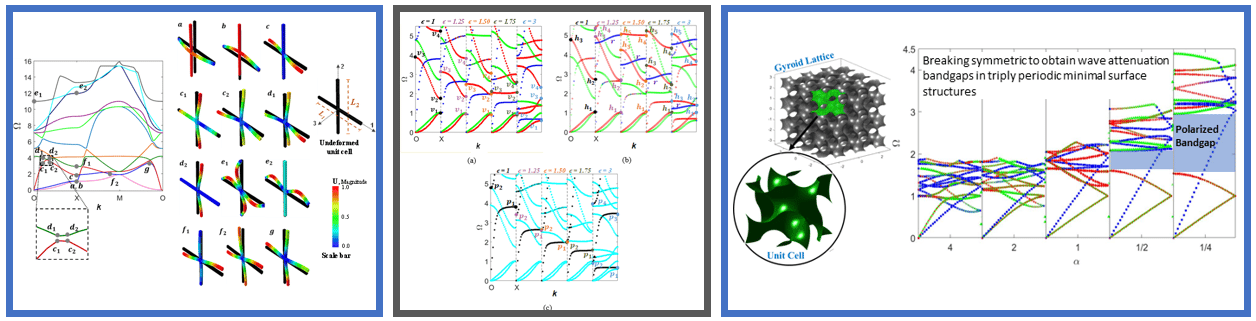
Periodic architected and phononic structures exhibit rich wave polarization characteristics which result in the generation of full, directional, or polarized wave attenuation bandgaps. Understanding the effect of the underlying geometrical and material characteristics on their elastic wave propagation behavior can help design lightweight engineering structures with bespoke wave functionalities. Further, understanding these relationships can also aid the development of non-destructive techniques based on elastic wave propagation. As part of this work, we are developing new mathematical tools that make it easier to identify wave polarizations and enable accurate identification of various wave attenuation bandgaps. Simultaneously, we are also investigating the fundamental dynamics of various lattice topologies to understand their emergent wave functionalities.
Status: Current
Funding: Wichita State University
Magic Phononic Structures
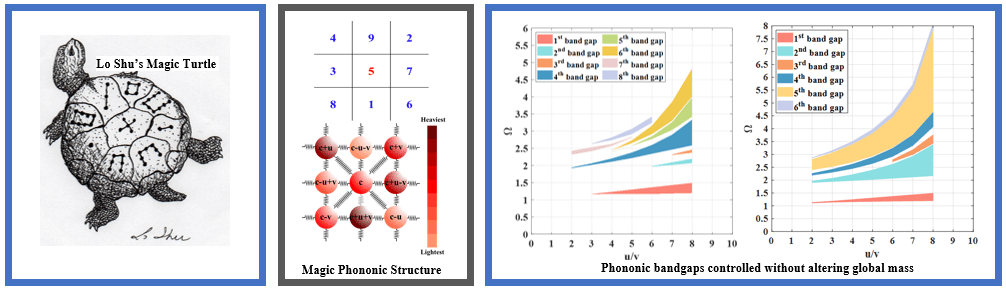
A magic square is defined as a square array of distinct positive integers arranged such that the sum along each individual row, column, and diagonal remains constant—referred to as the magic number. Said to have been initially discovered in China around 190 BCE, magic squares have historically been treated as a mystical or divine pattern by various cultures and can be routinely found on amulets, rings, talismans, and similar other protective charms. Over the past century, magic squares have transitioned from the spiritual realms to the world of recreational mathematics and make frequent appearances as puzzles and mind teasers. In this project, we leverage the concept of magic squares to design a new class of phononic structures that allow elastic wave bandgap tuning while preserving the global structural mass, stiffness, and moment of inertia. We are currently investigating the feasibility of this concept by studying the dispersion behavior of an idealized, infinite two-dimensional spring-mass system composed of a 3 x 3 unit cell of nine distinct point masses connected by linear springs of a constant stiffness. In this system, the point masses are arranged in a magic square pattern such that the total mass along each row, column, and main diagonal remains constant. Our results show that magic structures result in the generation of omnidirectional bandgaps, whose widths can be controlled by controlling the u/v ratio and without altering the overall system mass or stiffness.
Status: Current
Funding: Wichita State University
Lightweight Multifunctional Lattice Materials with Enhanced Impact Energy and Vibration Dissipation Properties for Space Structures
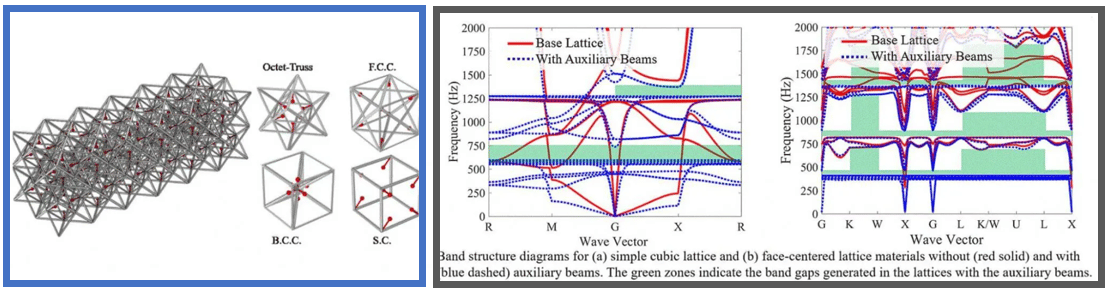
Improving the energy dissipation and vibration properties of lattice materials without significantly increasing their weight remains a key challenge towards their wider adoption for aerospace applications. To address this challenge, we are focused on the development of topological lattice materials based on the concepts of acoustic metamaterials and phononic structures. Acoustic metamaterials utilize the localized resonance of substructures added to the host structure to restrict the propagation of incident waves within frequency bands known as local resonance (LR) band gaps. Thus, the dynamic behavior of the metamaterial can be controlled by adjusting the behavior of the local resonant subsystem. The cellular architecture of lattice materials provides an excellent framework for the integration of locally resonant trusses for generating LR band gaps. Further, their periodic architecture causes interference effects which result in additional wave attenuation frequency regions classically referred to as phononic or Bragg band gaps. Formation of LR and phononic band gaps offers the possibility of effectively dissipating incident energy due to impact without inducing irreversible plastic deformation in the lattice material.
Status: Current
Funding: Wichita State University
Elastic Wave Propagation and Directivity in Hierarchical Structures
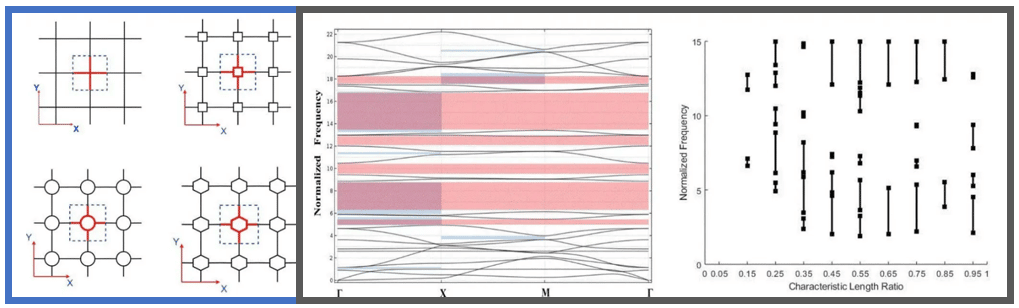
Hierarchical lattice structures offer a novel way of controlling the wave propagation behavior of engineering structures. Here, we are focused on understanding the effect of topological hierarchy on the bandgap and directivity behavior of lattice materials. Differences between self-similar and non-self-similar structures are of particular interest. As part of this work, we have developed a new technique to classify P- and S- waves propagating within the designed structure. The mechanism for generation of bandgaps were analyzed by studying the mode shapes for different characteristic length ratios. The effects of material symmetry for symmetric hierarchical lattices were analyzed, the results of which demonstrated that material asymmetry generates bandgaps at low frequency ranges. By observing the mode shapes of P and S waves, polarized bandgaps were identified to selectively suppress individual bands. Changing the material properties of hierarchical squares helps engineer individual P- and S-modes and generate directional bandgaps.
Status: Current
Funding: Wichita State University
Wave Propagation in Triply Periodic Minimal Surface Structures
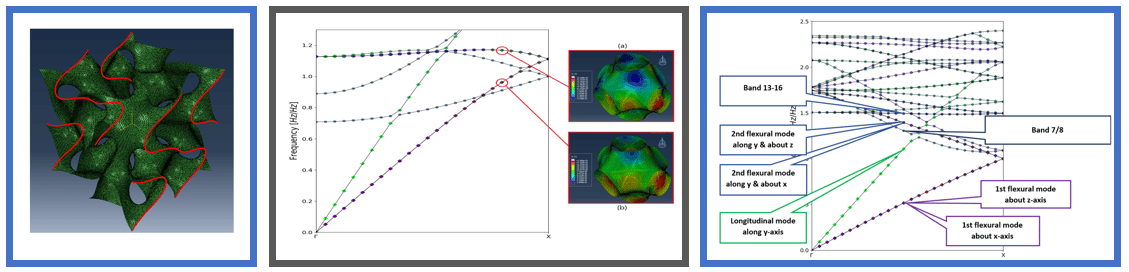
In this work, our goal is to delineate the dynamic behavior of structures with triply periodic minimal surfaces. While the stiffness and strength properties of such structures have recently been studied and shown to provide significant advantages over other topologies, their wave propagation behavior is still not completely understood. A significant challenge here is to efficiently apply periodic boundary conditions to complex three-dimensional surface models and leverage the benefit of unit cell models over computationally heavy time-domain analysis models. Here, we overcome this challenge by combining the modeling features of AutoCAD 3DS Max with python enabled Abaqus routines. An analysis of the unit cell was accomplished to determine and characterize the dispersion curves for Schwarz Primitive, Schwarz Diamond, Gyroid, Fischer Koch S, IWp, and FRD. The wave behavior of these structures shows significant differences. Current work involves exploring the effect of their topology on their directivity behavior.
Status: Current
Funding: Wichita State University
Meta-Phononic Sandwich Structures
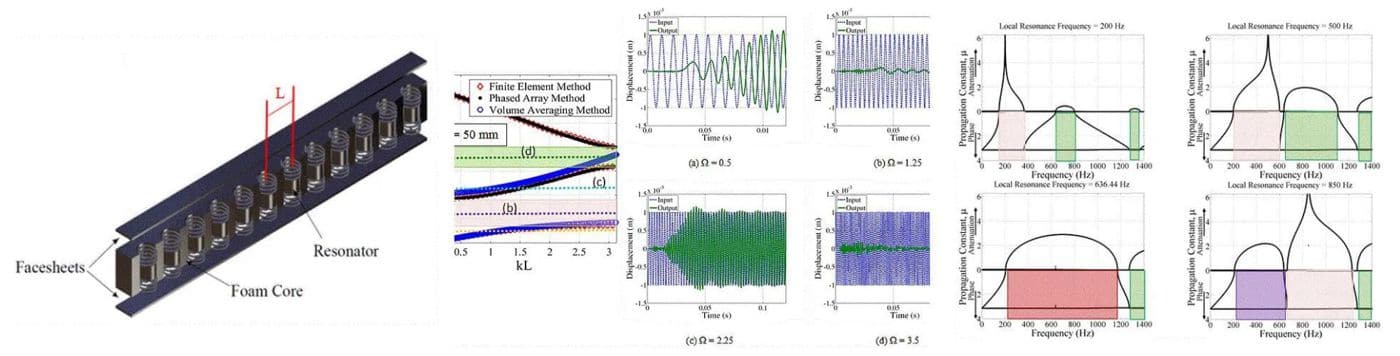
Typically, in structures containing local resonators, the resonators are embedded with a certain periodicity for manufacturing ease as well as to make analysis easier. Periodicity of the resonators allows for the creation of another wave attenuation band gap which is commonly referred to as a “Bragg” band gap. Thus, in order to completely understand the effect of addition of locally resonating elements to a structure, it is important to understand the effect of their inherent periodicity. This is accomplished by using various analytical methods such as the phased-array method, the transfer matrix method, etc. It is demonstrated that the periodicity of the resonating elements causes a change in the band structure and allows for further tailoring of the wave attenuation zones by tailoring the resonator parameters. The effect of addition of multiple resonators, with the same periodicity or with different periodicities is currently being investigated. A better understanding of the interaction between such band gaps could lead to structures exhibiting extremely wide wave attenuation zones and offering attractive dynamic properties without a significant mass penalty.
Status: Current
Collaborators: Prof. C. T. Sun (Purdue University)
Funding: Office of Naval Research
Dynamic Behavior of Sandwich Beams with Resonator Embedded Cores
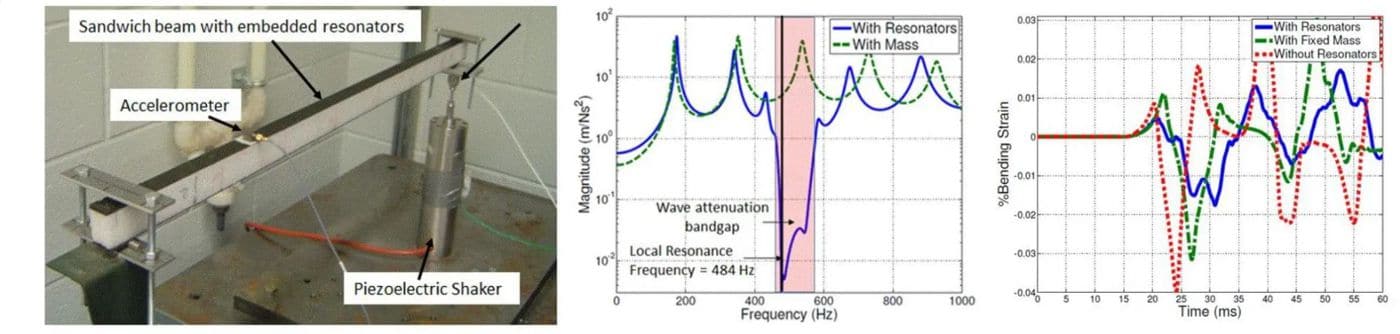
The aim of this research is to investigate the dynamic effects of inserting locally resonating elements into sandwich cores. Addition of such resonating elements allows the creation of a wave attenuation which may be tuned for a particular application by choosing the appropriate resonator parameters. A Timoshenko beam model is utilized to model the behavior of such sandwich beams. If modeled as a homogeneous elastic solid, the mass density of such a structure is found to be frequency dependent and it achieves negative values in certain frequency range. Sandwich beams with internal resonators may thus be treated as acoustic metamaterials and may be used to tailor the wave motion and produce anisotropic band gap structures. The presence of such a wave attenuation band gap has been demonstrated experimentally. It was also shown that such structures can be successfully deployed to improve the dynamic behavior of sandwich structures under hull slamming conditions as well as impact loads.
Status: Completed
Collaborators: Prof. C.T. Sun (Purdue University), Dr. J. S. Chen (National Cheng Kung University)
Funding: Office of Naval Research

